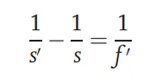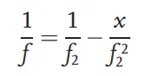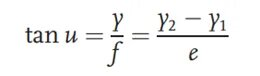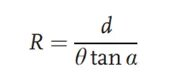1. Optikai rendszerek fókusztávolsága
A fókusztávolság az optikai rendszer nagyon fontos mutatója, a fókusztávolság fogalmát többé-kevésbé megértettük, itt áttekintjük.
Egy optikai rendszer fókusztávolsága, amelyet az optikai rendszer optikai középpontjától a nyaláb fókuszáig mért távolságként definiálunk, amikor párhuzamos fény esik be, a fény koncentrációját vagy divergenciáját méri egy optikai rendszerben. A következő diagrammal szemléltetjük ezt a koncepciót.
A fenti ábrán a bal oldalról beeső párhuzamos sugár, miután áthaladt az optikai rendszeren, az F' képfókuszpontba konvergál, a konvergáló sugár fordított hosszabbító vonala egy pontban metszi a beeső párhuzamos sugár megfelelő hosszabbító vonalát, és az ezen a ponton áthaladó, az optikai tengelyre merőleges felületet hátsó fősíknak nevezzük, a hátsó fősík a P2 pontban metszi az optikai tengellyel, amelyet főpontnak (vagy optikai középpontnak) nevezünk, a főpont és a képfókusz közötti távolságot általában fókusztávolságnak nevezzük, a teljes név a kép effektív fókusztávolsága.
Az ábrából az is látható, hogy az optikai rendszer utolsó felületétől a kép F' fókuszpontjáig mért távolságot hátsó fókusztávolságnak (BFL) nevezzük. Ennek megfelelően, ha a párhuzamos sugár jobb oldalról esik be, akkor léteznek a hatékony fókusztávolság és az elülső fókusztávolság (FFL) fogalmai is.
2. Fókusztávolság-vizsgálati módszerek
A gyakorlatban számos módszer alkalmazható optikai rendszerek fókusztávolságának vizsgálatára. Különböző elvek alapján a fókusztávolság-vizsgálati módszerek három kategóriába sorolhatók. Az első kategória a képsík helyzetén alapul, a második kategória a nagyítás és a fókusztávolság közötti összefüggést használja a fókusztávolság értékének meghatározásához, a harmadik kategória pedig a konvergáló fénysugár hullámfront-görbületét használja a fókusztávolság értékének meghatározásához.
Ebben a részben bemutatjuk az optikai rendszerek fókusztávolságának tesztelésére gyakran használt módszereket::
2.1Collimátor módszer
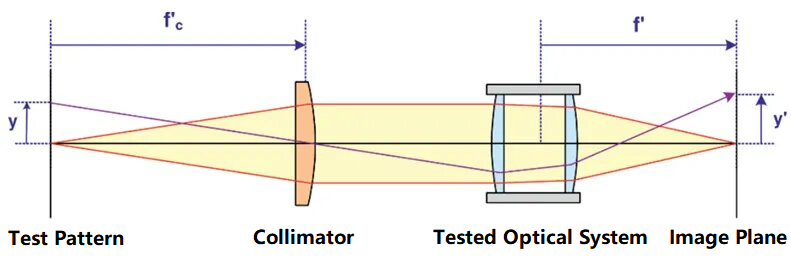
Az optikai rendszer fókusztávolságának kollimátorral történő vizsgálatának alapelve az alábbi ábrán látható:
Az ábrán a tesztminta a kollimátor fókuszpontjában helyezkedik el. A tesztminta magassága y és a fókusztávolság fcA kollimátor ' szöge ismert. Miután a kollimátor által kibocsátott párhuzamos nyalábot a vizsgált optikai rendszer konvergálja és a képsíkon leképezi, az optikai rendszer fókusztávolsága a képsíkon lévő tesztminta y' magassága alapján kiszámítható. A vizsgált optikai rendszer fókusztávolsága a következő képlettel számítható ki:
2.2 Gauss-eloszlásMmódszer
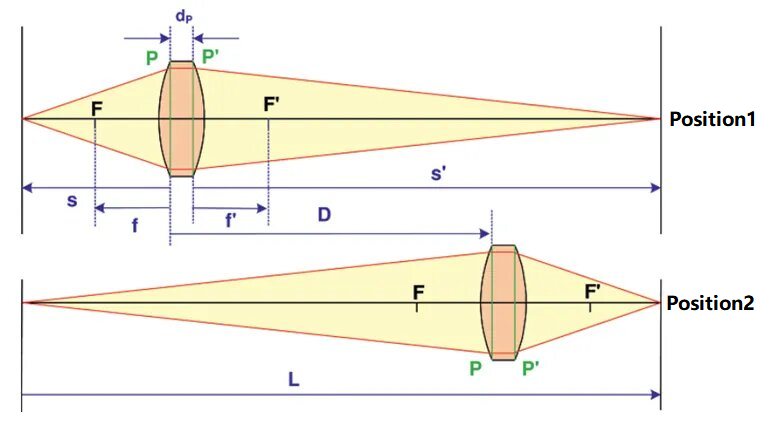
Az optikai rendszer fókusztávolságának vizsgálatára szolgáló Gauss-módszer vázlatos ábrája az alábbiakban látható:
Az ábrán a vizsgált optikai rendszer elülső és hátsó fősíkját P és P' jelöli, a két fősík közötti távolság pedig d.PEbben a módszerben a d értékePismertnek tekinthető, vagy értéke kicsi, és figyelmen kívül hagyható. Egy tárgyat és egy vevőképernyőt helyezünk el a bal és jobb szélen, és a köztük lévő távolságot L-ként rögzítjük, ahol L-nek nagyobbnak kell lennie, mint a vizsgált rendszer fókusztávolságának négyszerese. A vizsgált rendszer két pozícióban helyezhető el, amelyeket rendre 1-es és 2-es pozíciónak jelölünk. A bal oldali tárgy tisztán látható a vevőképernyőn. E két hely közötti távolság (D-vel jelölve) megmérhető. A konjugált kapcsolat szerint a következőt kapjuk:
Ebben a két pozícióban a tárgytávolságokat s1-ként és s2-ként rögzítjük, ekkor s2 - s1 = D. A képlet levezetésével az optikai rendszer fókusztávolságát az alábbiak szerint kapjuk meg:
2.3Lenzométer
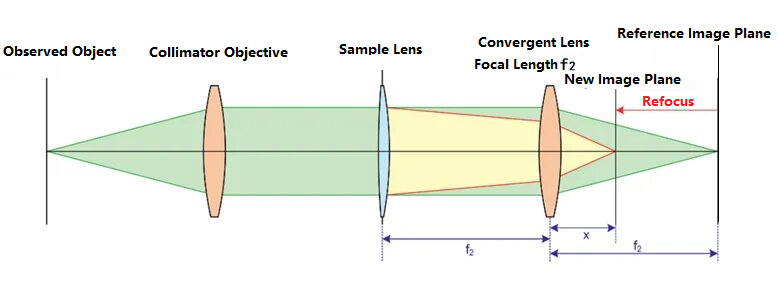
A lencsemérő kiválóan alkalmas hosszú fókusztávolságú optikai rendszerek tesztelésére. A vázlatos ábrája a következő:
Először is, a vizsgált lencse nincs az optikai útvonalban. A bal oldali megfigyelt céltárgy áthalad a kollimáló lencsén, és párhuzamos fénnyé válik. A párhuzamos fényt egy f fókusztávolságú gyűjtőlencse konvergálja.2és tiszta képet alkot a referencia képsíkon. Az optikai útvonal kalibrálása után a vizsgált lencsét az optikai útvonalba helyezik, és a vizsgált lencse és a gyűjtőlencse közötti távolságot f-nek kell tekinteni.2Ennek eredményeként a vizsgált lencse működése miatt a fénysugár újrafókuszálódik, ami a képsík helyzetének eltolódását okozza, és az ábrán az új képsík helyén tiszta képet eredményez. Az új képsík és a gyűjtőlencse közötti távolságot x-szel jelöljük. A tárgy-kép kapcsolat alapján a vizsgált lencse fókusztávolsága a következőképpen következtethető ki:
A gyakorlatban a lencsemérőt széles körben alkalmazzák szemüveglencsék felső fókusztávolságának mérésére, és az egyszerű kezelhetőség és a megbízható pontosság előnyeivel rendelkezik.
2.4 ApátRefraktométer
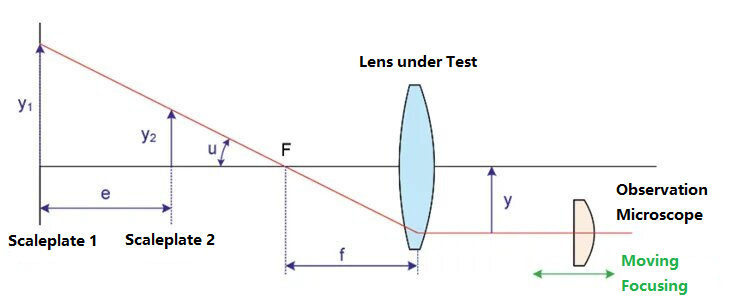
Az Abbe-féle refraktométer egy másik módszer az optikai rendszerek fókusztávolságának vizsgálatára. Vázlatos ábrája a következő:
Helyezzen két különböző magasságú vonalzót a vizsgált lencse tárgyfelület felőli oldalára, nevezetesen az 1-es és a 2-es vonalzólemezt. A megfelelő vonalzólemezek magassága y1 és y2. A két vonalzólemez közötti távolság e, a vonalzó felső vonala és az optikai tengely közötti szög pedig u. A vonalzólemezt a vizsgált lencse f fókusztávolsággal képezi le. A képfelület végén egy mikroszkóp van elhelyezve. A mikroszkóp helyzetének mozgatásával megtalálja a két vonalzólemez felső képét. Ekkor a mikroszkóp és az optikai tengely közötti távolságot y-nak jelöli. A tárgy-kép kapcsolat alapján a fókusztávolságot a következőképpen kapjuk meg:
2.5 Moire deflektometriaMódszer
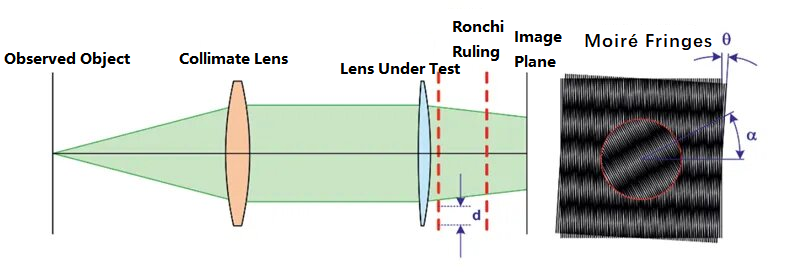
A Moiré-deflektometriás módszer két Ronchi-vonalat használ párhuzamos fénysugarakban. A Ronchi-vonal egy rácsszerű króm-fém filmminta, amelyet üvegfelületre helyeznek, és amelyet általában optikai rendszerek teljesítményének tesztelésére használnak. A módszer a két rács által létrehozott Moiré-sávok változását használja ki az optikai rendszer fókusztávolságának tesztelésére. Az elv vázlatos ábrája a következő:
A fenti ábrán a megfigyelt objektum a kollimátoron való áthaladás után párhuzamos sugárnyalábbal rendelkezik. Az optikai útvonalon, a vizsgált lencse előzetes hozzáadása nélkül, a párhuzamos sugárnyaláb két, θ elmozdulási szögű és d rácstávolságú rácson halad át, Moiré-csíkokat képezve a képsíkon. Ezután a vizsgált lencsét az optikai útvonalba helyezik. Az eredeti kollimált fény a lencsén történő megtörés után egy bizonyos fókusztávolságot hoz létre. A fénysugár görbületi sugara a következő képlettel számítható ki:
A vizsgált lencsét általában az első rácshoz nagyon közel helyezik el, így a fenti képletben az R érték a lencse fókusztávolságának felel meg. A módszer előnye, hogy pozitív és negatív fókusztávolságú rendszerek fókusztávolságát is képes vizsgálni.
2.6 OptikaiFiberAautokollimációMmódszer
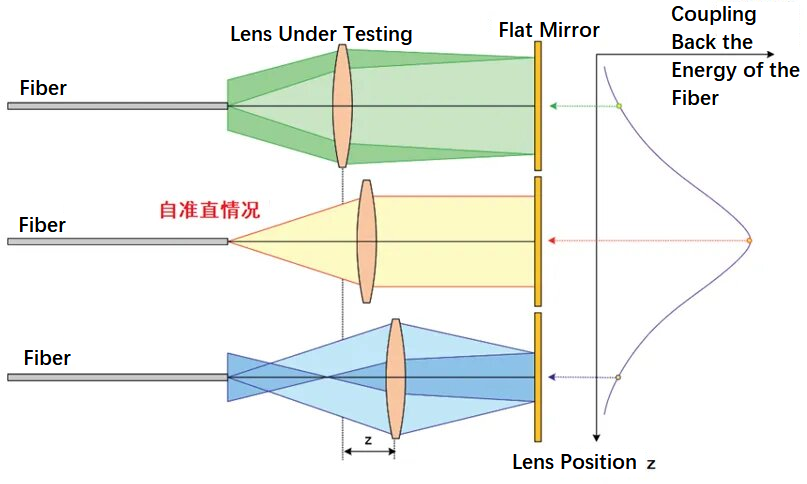
Az optikai szál autokollimációs módszerének lencse fókusztávolságának tesztelésére való alkalmazásának elvét az alábbi ábra mutatja. A módszer száloptikát használ egy divergens nyaláb kibocsátására, amely áthalad a vizsgált lencsén, majd egy síktükörre jut. Az ábrán látható három optikai út az optikai szál állapotát jelöli a fókuszon belül, a fókuszon belül és a fókuszon kívül. A vizsgált lencse helyzetének oda-vissza mozgatásával megtalálhatja a szálfej helyzetét a fókuszban. Ekkor a nyaláb önkollimálódik, és a síktükör általi visszaverődés után az energia nagy része visszatér a szálfej helyzetébe. A módszer elvileg egyszerű és könnyen megvalósítható.
3. Következtetés
A fókusztávolság egy optikai rendszer fontos paramétere. Ebben a cikkben részletesen ismertetjük az optikai rendszer fókusztávolságának fogalmát és annak vizsgálati módszereit. A vázlatos ábrával együtt elmagyarázzuk a fókusztávolság definícióját, beleértve a képoldali fókusztávolság, a tárgyoldali fókusztávolság és az elölről hátrafelé irányuló fókusztávolság fogalmait. A gyakorlatban számos módszer létezik az optikai rendszerek fókusztávolságának vizsgálatára. Ez a cikk bemutatja a kollimátoros módszer, a Gauss-módszer, a fókusztávolság-mérési módszer, az Abbe-féle fókusztávolság-mérési módszer, a Moiré-eltérítési módszer és az optikai szálas autokollimációs módszer vizsgálati alapelveit. Úgy gondolom, hogy a cikk elolvasásával jobban megérti az optikai rendszerek fókusztávolság-paramétereit.
Közzététel ideje: 2024. augusztus 9.